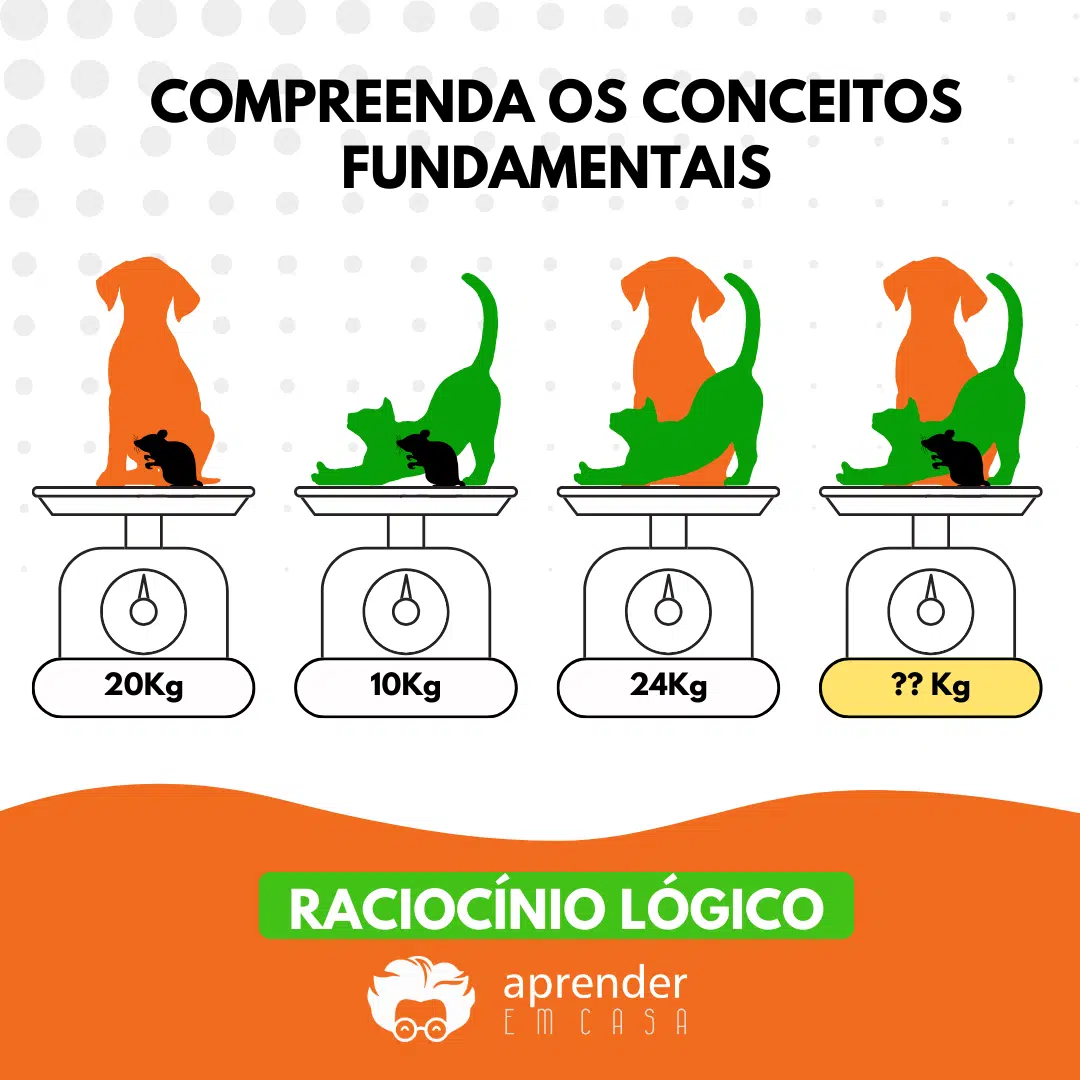
O raciocínio lógico é uma habilidade essencial para resolver problemas, interpretar informações e tomar decisões. Ele envolve a estruturação de argumentos, a análise de proposições e a determinação de conclusões baseadas em condições estabelecidas. Nesta leitura, exploraremos os fundamentos do raciocínio lógico, incluindo proposições, conectivos, tabelas verdade e operações lógicas, com exemplos para facilitar a compreensão.
O que são proposições?
As proposições são declarações que possuem um significado completo e podem ser classificadas como verdadeiras ou falsas. A lógica trabalha com esse tipo de sentença, classificando-a segundo dois princípios básicos:
- Princípio da Não-Contradição: uma proposição não pode ser simultaneamente verdadeira e falsa.
- Princípio do Terceiro Excluído: uma proposição deve ser verdadeira ou falsa; não existe uma terceira opção.
Exemplos de proposições:
- “O número 2 é primo.” (Verdadeiro)
- “Cinco mais três é igual a dez.” (Falso)
Por outro lado, nem toda frase é uma proposição. Sentenças interrogativas, como “Você gosta de café?”, e imperativas, como “Feche a porta!”, não podem ser classificadas como verdadeiras ou falsas.
Sentenças Abertas
Uma sentença aberta é aquela cujo valor lógico depende de variáveis. Por exemplo, a equação “x + 1 = 0” não pode ser classificada sem o valor de x. Se x = −1, a sentença é verdadeira; caso contrário, é falsa.
Conectivos Lógicos
Os conectivos conectam proposições simples para formar proposições compostas. Cada conectivo tem um significado específico, e seu valor lógico depende das proposições conectadas. Os principais conectivos são:
- E (∧): Verdadeiro somente quando ambas as proposições são verdadeiras.
- OU (∨): Verdadeiro se pelo menos uma proposição for verdadeira.
- NÃO (~ ou ¬): Inverte o valor lógico de uma proposição.
- SE… ENTÃO… (→): Falso apenas quando a primeira proposição é verdadeira e a segunda é falsa.
- SE, E SOMENTE SE (↔): Verdadeiro quando ambas as proposições têm o mesmo valor lógico.
Proposições Simples e Compostas
- Simples: Declarações únicas, como “O número 3 é primo.”
- Compostas: Conectam duas ou mais proposições simples, como “O número 3 é primo e o número 2 é par.”
Exemplos de proposições compostas:
- “Se o Brasil é um país continental, então os Estados Unidos também é.”
- “O número 4 é par ou o número 7 é primo.”
Tabela Verdade
A tabela verdade é uma ferramenta que ajuda a determinar o valor lógico de proposições compostas. Ela lista todas as combinações possíveis de valores para as proposições simples e calcula o resultado final.
Exemplo: para a proposição p ∧ q:
| p | q | p ∧ q |
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | F |
A conjunção p ∧ q só é verdadeira quando ambas as proposições p e q são verdadeiras.
Fórmula para determinar linhas na tabela verdade
A quantidade de linhas na tabela verdade é calculada pela fórmula 2n , onde n é o número de proposições simples. Por exemplo, para três proposições simples (p, q e r), a tabela terá 23 = 8 linhas.
Exemplo:
Proposição composta: (p → q) ∨ r
| p | q | r | p → q | (p → q) ∨ r |
| V | V | V | V | V |
| V | V | F | V | V |
| V | F | V | F | V |
| V | F | F | F | F |
| F | V | V | V | V |
| F | V | F | V | V |
| F | F | V | V | V |
| F | F | F | V | V |
Operações Lógicas
As operações lógicas definem o comportamento de cada conectivo em uma proposição composta:
Conjunção (p ∧ q)
Verdadeira apenas quando ambas as proposições são verdadeiras.
| p | q | p ∧ q |
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | F |
Disjunção (p ∨ q)
Verdadeira se pelo menos uma das proposições for verdadeira.
| p | q | p ∨ q |
| V | V | V |
| V | F | V |
| F | V | V |
| F | F | F |
Condicional (p → q)
Falsa apenas quando p é verdadeira e q é falsa.
| p | q | p → q |
| V | V | V |
| V | F | F |
| F | V | V |
| F | F | V |
Bicondicional (p↔q)
Verdadeira quando p e q possuem o mesmo valor lógico.
| p | q | p ↔ q |
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | V |
Negação (¬p)
Inverte o valor lógico de p.
| p | ¬p |
| V | F |
| F | V |
Tautologia, Contradição e Contingência
- Tautologia: Proposição composta sempre verdadeira.
- Contradição: Proposição composta sempre falsa.
- Contingência: Proposição composta que pode ser verdadeira ou falsa.
Exemplo de tautologia: p ∨ (¬p)
| p | ¬p | p ∨ (¬p) |
| V | F | V |
| F | V | V |
Finalizando
O raciocínio lógico é uma ferramenta poderosa, usada não apenas em Matemática, mas também na solução de problemas cotidianos e em exames. Dominar proposições, conectivos e tabelas verdade pode parecer desafiador, mas a prática é essencial para consolidar o aprendizado. Que tal começar agora com alguns exercícios práticos?